Compositionality

Dealing with Compositionality

This blog will introduce the research done in syntax that addressed compositionality. In one of the connectionist natural language processing papers I have read about, it touches on government binding theory proposed by Chomsky, and the paper tried to model the motion from d-structure to s-structure in GB theory through the non-overlap constraint and chain map combined with NNs.

And the demonstration of the non-overlap map is below

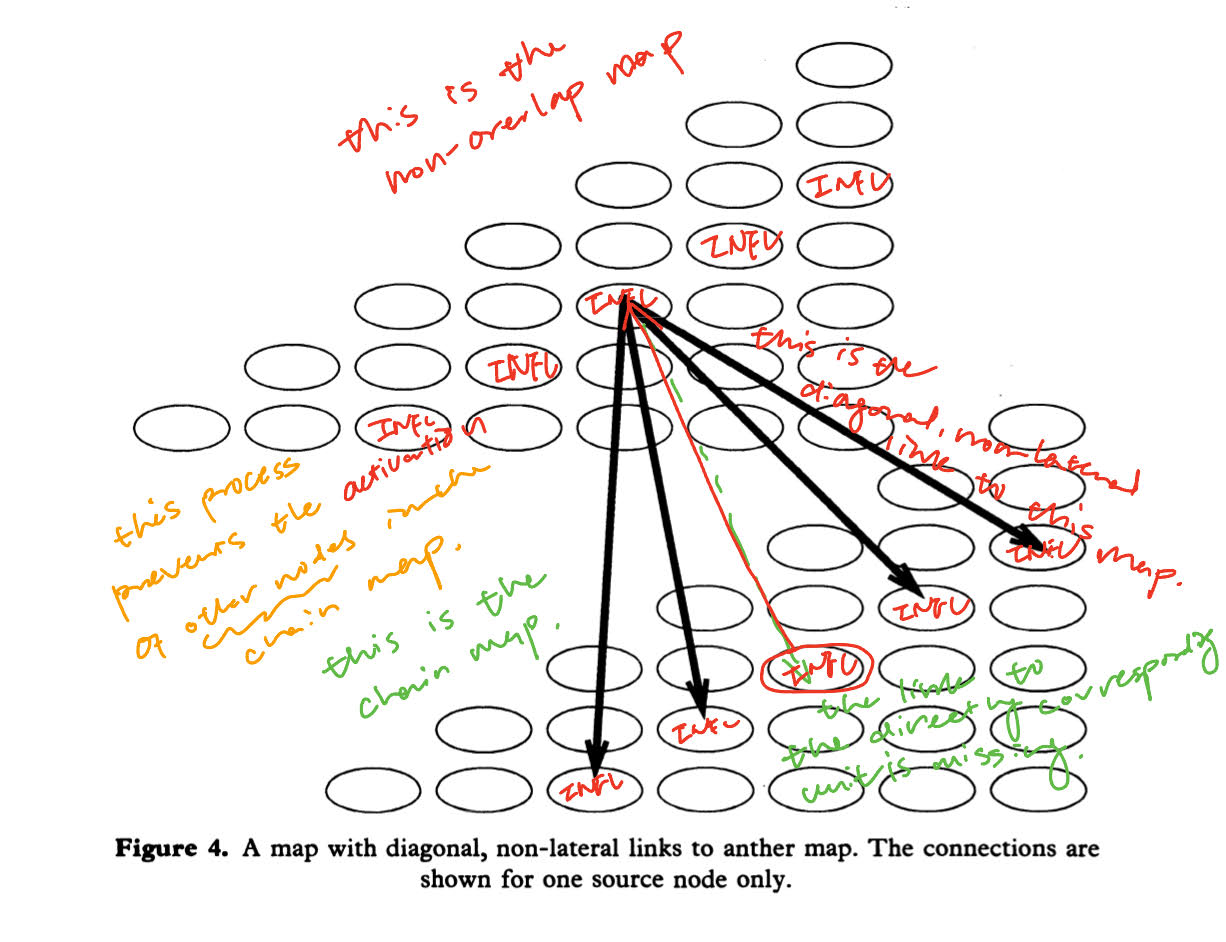
Non-Overlap Constraint Explained

The non-overlap constraint is a rule in cognitive models or neural networks that prevents overlapping activations of units in a chain map. This ensures that no two units representing the same syntactic marker can be active simultaneously, which helps maintain clear and distinct representations.

Diagram Breakdown

Components:

Chain Map (Green Text):

• Represents the initial activation of units.
• Units in this map correspond to elements or tokens that can be active.

Non-Overlap Map (Red Text):

• Corresponds to the chain map and enforces non-overlapping activations.
• Units in this map prevent other units in the same diagonal from activating.

Diagonal, Non-Lateral Inhibitory Links (Black Bold Arrows):

• These links prevent other units in the corresponding diagonal of the chain map from activating, thereby enforcing the non-overlap constraint.

Activation of Corresponding Unit In The Non-Overlap Map (Red Arrow)

• The red arrow or the lateral link indicates an activation process from the chain map where there is a unit activated. Correspondingly, there is a unit in direct parallel in the non-overlap map being activated.

Process:

1. When a unit in the chain map is activated, it activates its corresponding unit in the non-overlap map.
2. The active unit in the non-overlap map then inhibits all other units in the same diagonal in the chain map.
3. This ensures no two units in the chain map, which represent the same syntactic marker, can be active simultaneously.

Code Example with Explanation

Let’s look at a pseudo implementation that matches the diagram:

class Unit:
    def __init__(self, identifier):
        self.identifier = identifier
        self.active = False

    def __repr__(self):
        return f"Unit({self.identifier}, active={self.active})"

class Map:
    def __init__(self, name):
        self.name = name
        self.units = [[Unit(f"{name}{chr(65+i)}{j+1}") for j in range(5)]
                                                       for i in range(5)]

    def activate_unit(self, row, col):
        self.units[row][col].active = True
        print(f"Activating {self.units[row][col]} in {self.name} map.")
        self.enforce_non_overlap(row, col)

    def enforce_non_overlap(self, row, col):
        for i in range(5):
            if i != row:
                self.units[i][col].active = False
                print(f"Deactivating {self.units[i][col]} in {self.name}
                map due tonon-overlap constraint.")

# Initialize Chain Map and Non-Overlap Map
chain_map = Map("ChainMap")
non_overlap_map = Map("NonOverlapMap")

# Activate unit in Chain Map
chain_map.activate_unit(0, 0)

# Corresponding unit in Non-Overlap Map becomes active
non_overlap_map.activate_unit(0, 0)

# Output the state of maps
print("Chain Map State:")
for row in chain_map.units:
    print(row)

print("\nNon-Overlap Map State:")
for row in non_overlap_map.units:
    print(row)

Summary

Chain Map Activation:

• Activating a unit in the chain map triggers the corresponding unit in the non-overlap map.
• Example: Activating ChainMapA1 will activate NonOverlapMapA1.

Non-Overlap Map Enforces Constraint:

• The activated unit in the non-overlap map inhibits other units in the same diagonal in the chain map.
• This ensures that other units in the corresponding diagonal of the chain map remain inactive, preserving the non-overlap constraint.

Conclusion

By combining the visual diagram with the detailed code example, we’ve illustrated how the non-overlap constraint is implemented and enforced in a cognitive or neural model. The non-overlap map plays a crucial role in ensuring that units representing the same syntactic marker do not overlap in their activation, maintaining a clear and distinct representation of information.